母體指的是所有的數據,樣本指的是從母體抽樣的數據,舉例來說,一個班級有40人,它們的身高,40個身高數據,若只針對這個班,就是母體,但是,卻只是代表全校學生身高的一部分,也就是樣本。
回到「機率統計」頁面
回到「機率統計」頁面
樣本平均數(mean)不是母體平均數,樣本變異數(variance)也不是母體變異數,一個班40個人身高的平均數很難剛好是全校學生的身高平均數。
一個班40個人的身高變異數也不會是全校學生的身高變異數。
變異數計算
母體變異數的定義如下:
而樣本變異數的定義如下:
奇怪的地方
平均數
雖然樣本平均數不是母體平均數,不過,如果不斷重複從同一個母體抽樣平均,會得到一個近似母體平均數的數字。舉例來說,從一個學校所有學生中,不斷隨機選出40個學生取平均數,再將這些平均數平均,結果會接近直接算全校學生的身高平均數。
也就是說樣本平均數的期望值就是母體平均數:
變異數
樣本變異數跟母體變異數就沒這麼單純了。奇怪的地方是,為什麼樣本變異數公式的除術是n-1,而不是像平均數計算一樣用n?
為何樣本變異數要除的是(n-1)?
除數為n的話,變異數會太小
如果樣本變異數的除數是n,樣本變異數就會常常比母體變異數小。為什麼呢?
因為,樣本是從母體抽取的,抽樣的數據算出平均,並且抽樣的數據會相對的接近抽樣的平均,總不會剛好抽出的樣本平均數剛好是母體平均數,且樣本數據離樣本平均數就像母體數據離母體平均數一樣分散吧?
假設母體數據為0-99的整數,共100個數據,從中選出10個數字,然後計算樣本的平均數,分別用n及n-1當作除數算出變異數,連續執行200次,並將200個樣本平均數及200個樣本變異數平均。
也就是取得樣本平均數及樣本變異數的期望值,結果如下:
母體平均數 = 49.5
母體變異數 = 833.25
200個樣本平均數的平均:
200個樣本變異數的平均如下
使用n-1當除數:
使用n當除數:
用n-1當除數的結果就是數據較接近母體變異數。
其實,用n-1當除數的樣本變異數期望值就是母體變異數:
用自由度(degrees of freedom)解釋
樣本變異數必須用n-1當作除數也可用自由度來解釋。
自由度指的是抽樣過程中真正隨機的數據有幾個,假設我們知道母體平均數是3(只要一直抽樣取平均就可以獲得接近母體平均數的數字)。
假設總共擷取3個數據(n =
3),第1個數據隨機選取得到1,第2個數據隨機選取得到3,那麼第3個數據必須是5,這樣平均才是3。
真正隨機的數據只有2個,因此,這個樣本自由度就是2,也就是n-1。



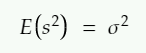

留言
張貼留言