我第一次開始投資股票,債券時,印象中是在美國執行上一次的升息循環時,結果,現在又讓我遇到第二次美國升息,因此我做了一些研究,針對美國升息期間,美股走勢的簡單分析。
2004年
在 2008 年美國次貸風暴前,美國也是在執行升息循環,當時,聯邦基準利率從 2004 年 6 月 14 日的 1%,一路升到 2006 年 6 月 24 日的 5.25%,真不巧,跟現在的聯邦基準利率一模一樣。
不過在升息期間,美國核心通膨 (PCE growth) 也不過才在 2% 左右而已,換句話說,當時美國的實質利率高達 3%,貨幣比現在還緊縮。
根據 The Fed in Action 網站資料,美國 2004 年通膨有升溫跡象,而失業率也逐漸從 2000 年金融風暴中恢復,因此聯準會升息。
這也說明了聯準會升息,也有可能不是只是根據手邊數據,也有可能是根據未來可能數據。
Inflation had started to increase somewhat in early 2004, and the unemployment rate had decreased to 5.3 percent in May 2004. So in August 2004, the Fed started a gradual increase of the target federal funds rate.
這段期間,標普 500 指數也是震盪向上。
2015年
上一次的升息循環在 2015 年底,當時的美國核心通膨更是低於 2%,不過美國還是升息,根據聯準會官方網站的資料,當時也是預測通膨會升溫,且就業市場良好,才會升息,並不是通膨已經超過目標的 2% 才升息。
In March 2015, the FOMC indicated in its postmeeting statement that it anticipated that it would be appropriate to raise the target range for the federal funds rate when it had seen further improvement in the labor market and was reasonably confident that inflation would move back to its 2 percent objective over the medium term...Inflation was especially low in 2015, held down by declines in energy prices and in prices of non-energy imports. However, with the economy having strengthened considerably, the FOMC is reasonably confident that inflation will move back to 2 percent as energy and import prices stabilize and the economic expansion continues.
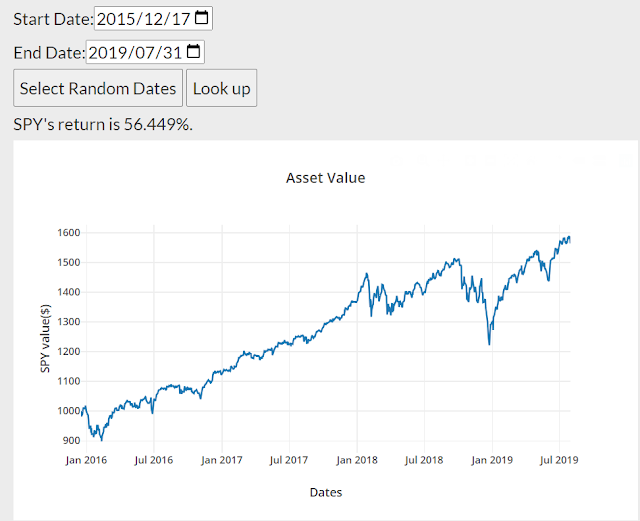
聯邦基準利率從 2015 年 12 月的 0% 升到 2019 年 4 月的 2.5%,也就是說,這段期間大部分美國是實質負利率,貨幣相對寬鬆,因此升息的目的,我想也是想讓利率達到中性水準。
這段期間,標普 500 指數也是震盪向上。
2022年
聯準會 2022 年 3 月開始了目前我們所經歷的升息,到了 2023 年 7 月美國才算正式進入實質正利率,也就是貨幣緊縮,到底未來通膨會不會就此開始下降,真的很難說,畢竟如果參考 2004 年的狀況,實質正利率都已經達到 3%,通膨還是不段緩緩上升。
將匯率納入考量
標普 500 指數歷史高點在 2022 年 1 月 3 日的 4796.56 點,何時會創新高無法預測,但是,如果將美金匯率納入計算,美股早就創新高。
- 2022 年 1 月 3 日美金匯率:27.632。
- 2022 年 7 月 28 日美金匯率:31.39。
- 2022 年 1 月 3 日 SPY 價格(經股利調整):466.41。
- 2022 年 7 月 28 日 SPY 價格(經股利調整):456.92。
投資 1 萬台幣,可以換成 10000 / 27.632 = 361.899美金,可以買進 0.775925 股 SPY,到了 2023 年 7 月 28 日,總價值為 0.775925 * 456.92 = 354.5357,換成台幣,354.5357 * 31.39 = 11,128.87,報酬率高過 11%。
我們看 00646 就知道了。
債券呢?
看起來,以台幣計價的話,只有 1 至 3 年的美國公債表現可以。
結論
美股在前 2 次美國升息期間,表現都是震盪向上,目前這一次就考量美金匯率而言,早已突破前高,這 3 次升息的共通點都是美國失業率很低,或許也是說明了美國經濟在這 3 次升息循環間的韌性,也導致了美股能夠震盪向上,當然,這也只是對於美國升息與美國走勢的粗淺分析,並沒辦法有效做關聯性。





留言
張貼留言